Larry Musa - Contravariance and Covariance, part 2

Contravariance and Covariance - Part 2

Josiah Willard Gibbs
Vector Calculus

Vector Concept 2 -- Vector Spaces

In the design of computer languages, the notion of contravariance and covariance have been borrowed from category theory to facilitate the discussion of type coercion and signature. Category theory, on the other hand, borrowed and abstracted the notion of contravariance and covariance from classical tensor analysis which in turn had its origins in physics.

In keeping with Feynman's observation that it is useful to have different ways thinking about known ideas, part 2 will be developing vectors from the point of view of linear algebra and vector spaces, which is a branch of algebra.

The axiomatic approach used in algebra requires the introduction of a number of definitions. However, only the definitions needed to illustrate contravariance and covariance in an abstract vector space will be given. So, unfortunately, for the sake of brevity, no detailed motivation of these mathematical concepts is going to be provided (*).

Needed Ideas From Linear Algebra

Vector Space
Linearly Independent
Span
Basis
Coordinates
Change of Basis
Linear Functional
Dual Space

The definition of a vector space also uses the algebraic concept of a field. (Not to be confused with a physical field, like, for example, the gravitational field...same words, different concepts.) For those who have not studied fields and do not wish to, good examples are the real numbers R, or the complex numbers C, which can be substituted in the definition below to allow you to follow along. Boldface is used to indicate elements of the vector space, normal font is used to indicate scalars

We now introduce some notation, and a convention, that will be useful. The Kronecker delta is defined by:

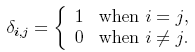Also, the Einstein summation convention will be used. That is, whenever repeated indices appear in an equation, it is understood that a summation is taken over these repeated indices.

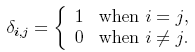
Vector Space

A vector space V consists of a set of objects, called vectors, and a field F, called scalars , and a binary operation + on vectors, that satisfies the following axioms:

i) if a and b are vectors, then so is a +b for all vectors a and b
ii) a+ b =b + a
iii) a + (b + c) = (a + b) + c
iv) There is a zero vector, 0, such that 0 + a = a + 0 = a for any vector a
v) There are additive inverses. For each vector a, there exists a vector -a such that a + (-a) = -a + a = 0.
vi) Scalar multiplication. For any scalar k and any vector a, k a is a vector.
vii) k(a + b) = ka + kb
viii) (k + l)a = ka + la for any scalars k and l
ix) k(l(a)) = kl(a) for any scalars k and l
x) 1a = a1 = a where 1 is the scalar identity

Linear Independence

A set of vectors {v₁,...,v_k} is linearly independent iff
a₁v₁ + ... + a_kv_k = 0 implies a₁=...=a_k= 0

Span

The span of a set of vectors {v₁,...,v_k} is the intersection of all subspaces that contain {v₁,...,v_k}

A straightforward result is that the span of a set of vectors {v₁,...,v_k} is given by all possible linear combinations of the {v₁,...,v_k}. This result is often more useful to work with than the actual definition.

Basis

A basis for a vector space is any set of linearly independent vectors that span V.

Given a basis for V, the number of vectors in the basis is called the dimension of V. A finite dimensional vector space is a vector space that is spanned by a finite number of vectors. The discussion will be limited to finite dimensional vector spaces.

Coordinates

Let v be a vector in V, and let β = {v₁,...,v_n} be an ordered basis for V. Then if v = a¹v₁ + ... + aⁿv_n , the scalars a¹,...,aⁿ are called the coordinates of v with respect to the basis β, and is written as a nx1 column matrix: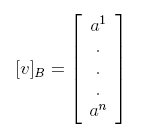

Change of Basis

We do not wish to be constrained to one basis. If we formulate an equation that uses coordinates in its formulation, we would like to know that it is true independent of the basis chosen. Therefore, we need to know how to express our equation in a new basis. Also, it is often the case that we are able to transform to a new basis where our equations take on a simpler form. For these reasons, it important to study the change of basis problem.

Let

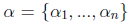be a basis for V and v be an arbitrary vector with coordinates

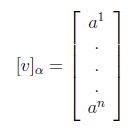If we now instead wish to use a different basis

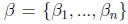how do we calculate the new coordinates?

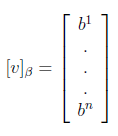
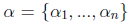
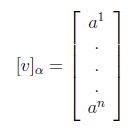
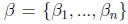
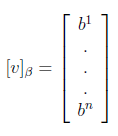
To answer this question, expand v in the beta basis, using the cordinates just given:

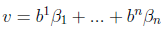Then, writing this in coordinate form in the alpha basis gives

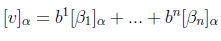This can be re-written as a nxn matrix times a nx1 matrix as

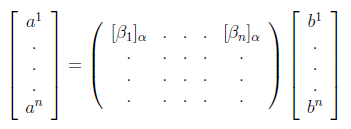
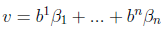
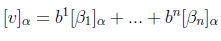
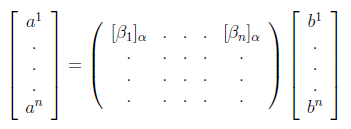
where the nxn matrix's columns are the coordinates of the beta basis vectors with respect to the alpha basis. Denoting the nxn matrix, by P, this can be written as

v_α = P v_β

and left multipling by P^-1 gives the require expression for the coordinates of v in the new basis:

v_β = P^-1 v_α

The matrix P is called the transistion matrix from the α basis to the β basis.

( A word on convention: if instead of expanding v in the β basis above, I had expanded v in the α basis, and taken coordinates in the β basis, I would have finally arrived at a slightly different form:

v_β = Q v_α

where Q is the matrix formed by the coordinate vectors of the α basis vectors with respect to the β basis. Occasionally, people call Q the transition matrix. If you are reading a book on linear algebra you need to check the convention being used.)

Having provided most of the needed definitions, we are very close to having all language needed to state the main idea. Recall in the "directed arrow" definition of a vector, the contravariant components of a vector were its coordinates with respect to the reciprocal lattice, and the reciprocal lattice was defined by the requirement eⁱ^.e_k = 0. In the abstract vector space formulation, this notion is generalized by the concept of the dual space and dual basis, which we now introduce.

Linear Functional

Definition: A linear functional on a vector space V is a linear map from V into the scalars K.

Dual Space and Dual Vectors

The set of all linear functionals on a vector space V is called the dual space of V, denoted by V^*. Elements of the dual space are called dual vectors .

If V is a vector space of dimension n, then V^* is a vector space of dimension n. Given a basis α for V, we construct a basis for V^*as follows:

Dual Basis

For a given basis α,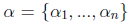

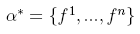
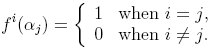
the set of linear functionals,

defined by

is a basis for V*, called the dual basis of α .

We now know how to get a basis for V^* given a basis for V . This allows us to write the components for an aritrary dual vector. We now want to enquire how the coordinates of our arbitary dual vector change when a change of basis is performed is performed in V. The change of basis induces a change of basis on the dual space.

Old Bases	New Bases

The key to discovering how dual vectors transform is to require that the new dual basis vectors, gⁱ, satisfy

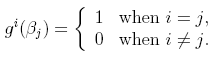Let the transformation matrix to the new dual basis be h_ik. Then gⁱ=h_ikf^k, where the Einstein summation convention is used to indicate a summation is taken over the indices k. If β_j = Q_jlα_l then we have

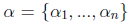
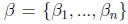
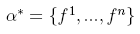
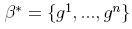
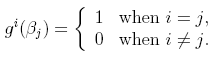
h_ikf^kQ_jlα _l= δⁱ_j

Using the summation convention and simplifying this reduces to

h_ikQ_jlδ^k_l = δⁱ_j

and simplifying one more time gives

h_ilQ_jl= δⁱ_j

or in other words

h_ilQ^T_lj= δⁱ_j

where Q^T is the transpose of Q.

Thus we have the important result that

h = (Q^T)^-1

So, the coordinates in the new dual basis are computed from the change of basis matrix by taking the transpose inverse of the transformation matrix and using that as the transformation matrix for the dual vectors. The dual vectors are also called contravariant vectors, and the vectors in the original space are called covariant vectors. The contravariant vectors are said to transform contragrediently and the covariant vectors transform cogrediently.

Next week -- Tensor analysis and vector transformation laws.

(*) Starting with part 2, the discussion becomes more abstract. I cover quickly what is usually covered at a more leisurely pace in advanced linear algebra coures. I recommended "Linear Algebra" by Kunze and Hoffman as a reference, and also Schaum's Linear Algebra for practice problems.

There are other possible reference books (for example, Strang's unfortunate text "Linear Algebra and Its Applications") on linear algebra, but they devote a lot of time to other topics before even getting to linear transformations, which is the heart of the linear algebra. Kunze and Hoffman is the standard reference. The problem with Strang is a student can take a linear algebra course using his text, and not understand the centrality of linear transformations because Strang spends so much time on other, and easier, topics. Solving equations using matrices with either matrix multiplication , or Gaussian elimination techniqes, which Strang devotes much time to is rather trivial. In fact, these topics I have successfully taught to a 9 year old. Vector spaces, basis, and linear transformations is more demanding.